2011同等学力申硕考前30练：计算机综合数学

    一、形式化下列语句

    1. 有的实数不是有理数，但所有的有理数都是实数。

    2. 对于任意实数都存在比它大的实数 .

    3. 若那套房子有三室一厅，并且居住面积在90平米以上，老王就要那套房子。

    4. 每位父亲都喜欢自己的孩子。

    二、填空

    1. 设p：1＋1＝5，q：明天是阴天，则命题"只要1＋1＝5，那么明天是阴天"可符号化为_____________，其真值是________.

    2. 在公式（  z）（P（z）→Q（x，z））∧（  z）R（x，z）中，  z的辖域是___________________， z的辖域是__________________.

    3. 设R为非空集合A上的二元关系，如果R具有自反性。___________.__________则称R为A上的一个偏序关系。

    4. 设x＝{1，3，5，9，15，45}，R是x上的整除关系，则R是x上的偏序，其最大元是___________，极小元是_________.

    5. 给定命题公式（P∨Q）→R，该公式在联接词集合{  ，→}中的形式为__________，在联接词集合{  ，∧}中的形式为__________ .

     6. 设 ， 中可定义_______个函数，其中有_________个满射函数；

     可定义_______个函数，其中有_________个单射函数。

    7. 设x＝{1，3，5，9，15，45}，R是x上的整除关系，则R是x上的偏序，其最大元是_________，极小元是______.

    8. 6名志愿者分配到5个西部学校支教，每个学校至少1人，共有_____种不同的分配方式。

    三、判断下列推理式及集合。关系运算的正确性

   1. （P→Q） （P→R）   P →（Q  R） （   ）

    2. （P Q）→R  （P→R）  （Q→R） （   ）

    3. 一个关系可以：既不满足自反性，也不满足非自反性。（   ）

    4. 一个关系可以：既不满足对称性，也不满足反对称性。（   ）

    5. 一个关系可以：既满足对称性，同时也满足反对称性。（   ）

    四、计算和证明

    1. 设个体域D＝{2，3，6}，F（x）：x≤3，G（x）：x>5，消去公式 x（F（x）∧ yG（y））中的量词，并讨论其真值。

    2. 用等值演算法求公式 （p→q）→（p→q）的主合取范式。

    3. 设A=  ，（1）求P（A）；（2）写出P（A）上的包含关系 .

    4. 设  ，从A到B不同的二元关系有多少个？ 又有多少种不同的函数？

    5. 设 ，在A×A上定义关系R：如果a+d=b+c， 则<a， b>R<c， d>.（1）证明R是等价关系。（2）求[<3，6>]R .

    6. 设 ，R是集合A上的整除关系： R＝{<x，y>| x整除y }.（1）证明R是偏序关系； （2）画出相应的哈斯图。

    7. 设A＝{a，b，c}，求A上所有等价关系。

    8. 所有的主持人都很有风度。李明是个学生并且是个节目主持人。因此有些学生很有风度。请用谓词逻辑中的推理理论证明上述推理。（个体域是人）

    9. 求  的主析取范式。

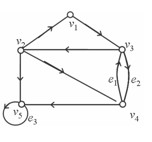
    10. 有向图D=<V，E>如图所示

    1）D中有多少条不同的初级回路；

    2）求v1到v4的短程线与距离；

    3）判断D是哪一类连通图。

    11. 求由2个0.3个2和3个5构成的八位数共有多少个？

    12. 一棵无向树T中有ni个顶点的度数为i， i=1，2，3，…，k，其余顶点都是叶子，试计算T中的叶子数。

    13. 证明题构造下面推理的证明：

    前提： 

    .结论：  

    下载原题： 

  2011年同等学力计算机综合数学.doc

8c89225f85d7bf66aa495cad89402cdc.doc (63.50 KB)