考研数学：洛必达法则求抽象函数极限易犯错误

 　　考研数学：洛必达法则求抽象函数极限易犯错误

　　函数极限的计算是考研数学中的一个高频考点，每年都会出题。计算函数极限的方法很多，如：利用极限的基本性质、两个重要极限、等价无穷小代换、洛必达法则、泰勒公式、恒等变形等，其中洛必达法则是重要的方法之一，经常用于函数极限的计算之中，但有些同学在运用洛必达法则时容易出现错误，没有正确掌握其使用方法，下面文都教育考研数学的蔡老师对使用洛必达法则求抽象函数的极限时容易犯的错误做些分析，供考研的同学复习参考。

　　一、使用洛必达法则求抽象函数的极限时容易犯的错误

　　对于抽象函数的极限，运用洛必达法则计算时容易出现下面这样的错误：

1、题目条件只是告诉了函数

连续，并未说明可导，因此，在求极限过程中运用洛必达法则对函数进行求导是错误的; 2、题目虽然告诉了函数

可导，但不知导数是否连续，因此，把导函数当成连续的函数来求极限是错误的。

　　下面通过一些具体例题来说明这些错误是如何发生的，以及应该怎么避免。

　　二、典型题型分析

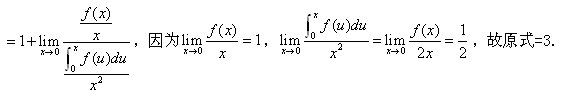
　　上面的分析和具体例题提醒我们，虽然洛必达法则是一个很有用的、重要的求函数极限的工具，但在运用洛必达法则求函数极限时，一定要仔细审视函数是否满足洛必达法则的使用条件，不要理所当然地认为或默认所有函数都符合其运用条件，尤其是求抽象函数的极限时要特别小心，不要出现不该犯的错误，从而导致在考试中丢分。

　　关键词：考研数学 洛必达法则 函数极限