2017考研数学:二阶常系数线性非齐次差分方程的通解分析

     2017考研数学:二阶常系数线性非齐次差分方程的通解分析

    差分方程除了用于对离散变量建立离散数学模型外，也可用于将连续变量及其连续数学模型离散化，换句话说，就是将微分方程离散化为差分方程，这对于难以求出精确解的微分方程来说具有重要的作用，事实上微分方程的数值解法就是如此，它通过差分方程来求出微分方程的近似解。在这里文都考研数学老师对二阶常系数线性非齐次差分方程的求解方法做些分析总结，供有兴趣的2017考研的同学拓展思路参考。

　　一、二阶常系数线性非齐次差分方程的通解

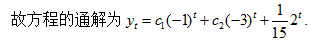
从前面的分析我们看到，二阶常系数线性非齐次差分方程的通解与二阶常系数线性非齐次微分方程的通解有非常相似的结论，比如其通解都是其特解与对应齐次方程的通解之和，而齐次方程的通解可以通过特征根求出，对于几类常见的自由项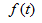类型，包括：多项式、指数函数及二者乘积，其相应差分方程的特解也与微分方程的情形很类似，当然，二者还是有有些差别的，这一点希望大家注意。